로짓: 통계연습 - 김두얼 교수 편
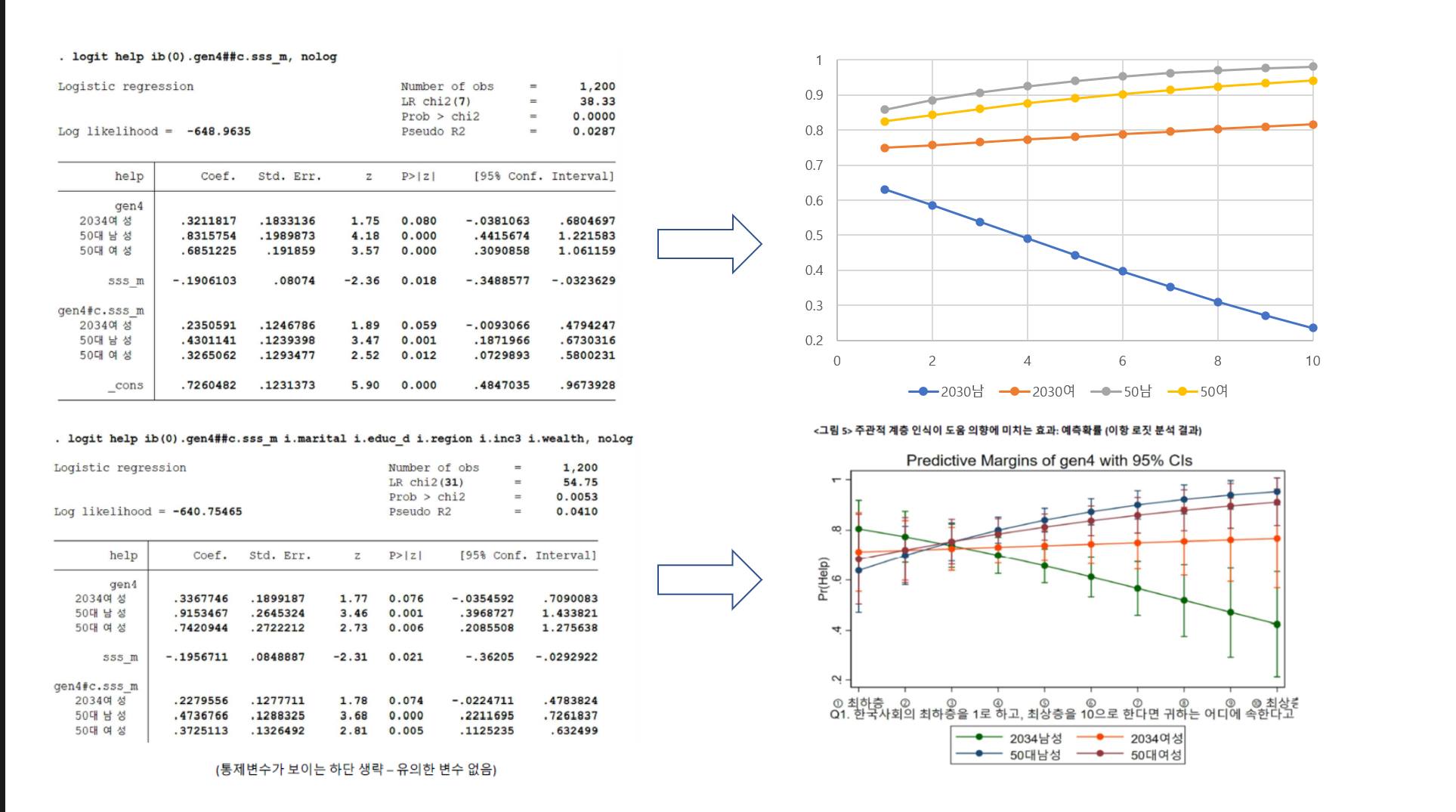
여진이 계속되니, KBS 보도 관련 더 안쓰겠다는 말은 못하겠고, 이 번 논란의 당사자 중에 한 분인 김두얼 교수가 오늘 페북 포스팅에서 통제변수 없는 로짓 모델로 그래프를 그리면 그래프가 아래 그림의 첫번째와 같이 나온다고
"그 동안의 경험에 비추어보건데, 그리고 위 두 그림을 비교해 보건데, 저자들이 제시한 그림은 원자료의 실체와는 상당히 거리가 있을 것 같다는 생각이 듭니다." "아울러 길게 설명드리기는 어렵지만, 분석에서 초점을 맞추는 두 변수 외의 통제변수 때문에 이 정도로 그림에 변화가 오는 건 제 상식으로는 납득하기 어렵습니다."
라면서 뭔가 KBS 보도 연구진의 의도가 있다는 식으로 얘기한다.
비즈조선(조선비즈인가?) 조모 선생만으로도 피곤한데, 여러명의 안티소비던스를 만들 것 같지만, 로짓 공부하는 학생들에게 도움이 되는 teachable moment이기에 어쩔 수 없이 제가 총대를 매고 김두얼 교수의 이 그래프가 왜 잘못되었는지 지적하고자 한다.
저도 의심이 많은지라 통제변수 없는 로짓결과로 김두얼 교수와 똑같이 그래프를 그려봤다. 그랬더니 김두얼 교수가 그린 그래프처럼 나오더라. 이렇게 나오면 안된다. 그래서 연구진들이 데이터에 무슨 조치를 취한 건지 reverse engineering을 해봤다.
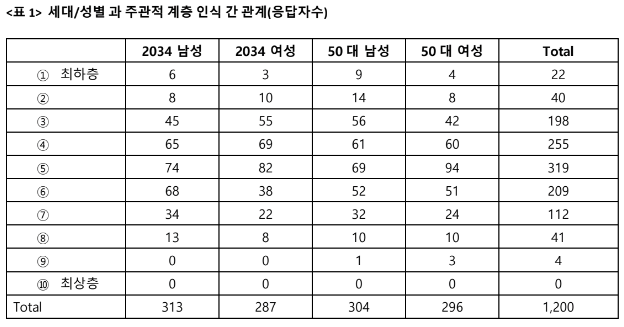
리버스 엔지니어링을 할려면 기준점이 있어야 한다. 내가 한 계산이 맞는건지 확인할 수 있는 기준점. 그런데 그 기준점은 <표 3>이다. 이 표에서 20-34 남성 중 그렇다는 응답이 0.112 + 0.553 = 0.665다. 통제변수 없는 로짓으로 계산해서 이 숫자를 재현해야 한다.
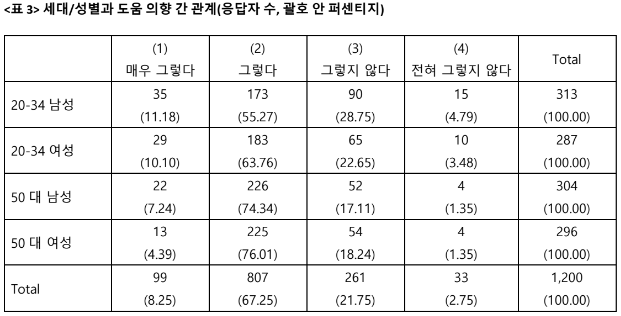
아래는 로짓 공부하는 학생들을 위한 시험 문제다. 한 번 해보시라. 이걸 어떻게 하는지 바로 아이디어가 떠오르지 않는다면 로짓 잘 모르는거다. 연습 좀 더 해야.
==========
(1) 아래 로짓 결과표를 이용하여 <표 3>의 타인 도움 의향 (1)+(2)의 4개 그룹별 정확한 (오차범위 0.005 포인트 이내) %를 reverse engineering으로 도출하시오.
(2) 아래 로짓 결과표에서 절편값(_cons)의 정확한 의미를 해석하시오. 수학적 의미 뿐만 아니라 <표3>과 연관된 해석을 제공하시오.
힌트: 연구진들이 SSS(주관적 계층 인식) 변수를 변형하였음.
==========

답:
==========
1. 저자들은 주관적 계층인식의 grand-mean centering 값으로 sss_m를 사용한 것으로 보임 (저자들에게 물어본거 아니고 , 통계 분석 제대로 했는지 확인할려고 제가 계산해 본 것, 그 후 연구진 설명서를 올린 임동균 교수 페북에서 질문해서 확인). 따라서 그룹별 SSS값의 4개 그룹 grand-mean과의 격차를 계산하고 이 격차값을 위 로짓통계치에 대입하여 p = exp(xB)/(1+exp(xB))로 확률을 계산하면 표3의 그룹별 (1)+(2)값이 모두 산출된다.
예를 들어 20-34세 남성의 주관적 계층 인식 평균은 4.911인데, 4개 집단 전체의 평균은 4.761이다. 따라서 20-34세 남성의 타인조력 의향평균은 exp(.726-.191*(4.911-4.761)/(1+exp(.726-.191*(4.911-4.761))로 계산해야 한다. 그러면 .665가 나와서 <표 3>의 수치와 일치한다.
김두얼 교수 식으로 grand-mean centering에 대한 고려없이 exp(.726-.191*4.911)/(1+exp(.726-.191*4.911))로 계산하면 .447이 나온다. 20-34세 남성의 타인 조력의향이 45%밖에 안되는걸로 잘못 계산하게 된다.
2. 따라서 절편값은 SSS값이 grand-mean 일 때 기대되는 20-34세 남성 오즈의 로그 전환(=로짓)값이다. 그러니까 20-34세 남성이 4개 집단 전체의 평균 SSS를 가지면 조력 의향은 exp(.726)/(1+exp(.726)) = .674이다.
참고로 2034여성/50대남/50대여 등 그룹 주효과는 SSS값이 grand-mean 일 때 기대되는 오즈"비"의 로그 전환 값이다. 절편은 오즈고 다른 계수는 오즈"비"라는게 포인트다.
==========
연구진이 올린 설명에서 로짓 통계표의 Stata 코맨드에서 "sss_m"라고 되어 있는데 이 변수는 <표 1>의 SSS 점수 전체의 grand mean을 낸 후에 각각의 응답에서 이 값을 빼 준 것이다.
이렇게 mean-centering을 하는 이유는 자칫하면 아무 의미없는 숫자가 될 수 있는 절편의 값에 의미를 부여하기 위해서이다. 대단히 보편적으로 사용되는 기법이다. 로짓에서 뿐만 아니라 OLS에서도 절편에 의미를 부여할려면 이와 비슷한 centering 조치를 취한다. 또한 위 로짓에서 각 그룹의 주효과는 그룹별 절편의 변화량이다. grand mean centering을 해줌으로써 각 그룹의 SSS 점수가 grand mean 값으로 동일할 때 그룹 간 격차는 얼마인지를 알 수 있다.
로짓은 오즈비의 로그값이기 때문에 모든 숫자가 비교 대상이 되는 베이스 라인에 따라 의미가 달라진다. 준거집단인 20-34세 그룹의 절편값에 의미를 부여하고 다른 집단과 비교함으로써 집단간 평균 격차를 알 수 있다.
어쨌든 그렇게 해서 통제변수 없을 때 제가 도출하는 그래프는 아래와 같다.
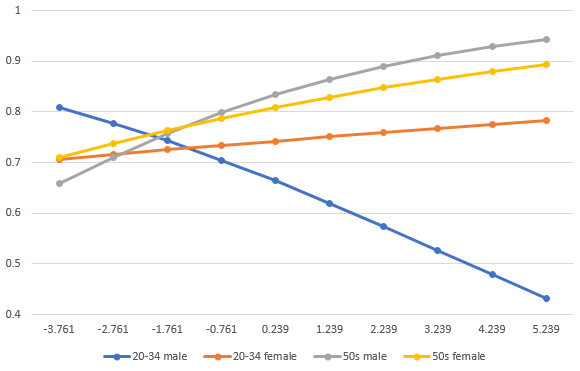
Ps. 기본적으로 타 연구자에 대한 존중 의식을 가져야 한다.